Фрактальное искусство: современная математика, искусство Природы и природа Искусства

Наука всегда пыталась объяснить законы, лежащие в основе природы. И в то же время понимание природы остаётся некой, порой недостижимой, целью как для науки, так и для искусства. На протяжении всей истории человечества совершенная природная форма рано или поздно поднималась на свой законный пьедестал абсолютного идеала красоты. Человек мог только стремиться копировать природу, но никогда не достигал её сложности и совершенства. Сегодня, когда современное искусство выдвинуло природу на передний план художественных достижений (мыслимых как её олицетворение и должных существовать по её законам), современные технологии предоставили обеим сторонам отношения «наука-искусство» подходящие инструменты для достижения их общей цели. В самом центре треугольника «искусство-наука-технология» располагается фрактальное искусство, которое связано с понятием фрактала, фрактальной геометрией и теорией хаоса. Как следствие, возникла необходимость в осмыслении новых перспектив, открывающихся благодаря фрактальной геометрии, чтобы понять, какие новые экспансивные возможности для искусства даёт изучение фрактального характера природы.

Математика всегда влияла на искусство. Такие математические понятия, как золотое сечение, платоново тело и проективная геометрия, широко использовались художниками и скульпторами, а пифагорейское арифметическое восприятие гармонии доминирует в западной музыке и по сей день. Бесконечность и теория вероятности вдохновили таких художников, как М.К. Эшер, и таких композиторов, как Янис Ксенакис, сформировав тенденции в современном искусстве и музыке. Развитие технологий создало новые области пересечения математики и искусства: цифровое искусство, компьютерная музыка и новые медиа.

Основание теории хаоса познакомило математику с новой увлекательной и интригующей реальностью – самой природой. До этого ученые могли лишь наблюдать нелинейный динамический характер природных структур и процессов. Теперь у них появились математические инструменты для описания, объяснения и доказательства хаотических свойств природы, таких как погодные системы и эффект бабочки. Компьютеры стали неотъемлемой частью этой научной революции, поскольку они способны рассчитывать нелинейные динамические системы и визуализировать результаты во времени; ученые могут наблюдать хаотическую эволюцию природного явления на экране компьютера.

Появились эксцентричные формы, неправильные геометрические объекты и необычные фигуры; открылся мир, в котором нереальное (графические представления алгоритмических процессов) подразумевало реальное (природу). Бенуа Мандельброт был первым математиком, оформившим эту новую область в самостоятельную теорию, которая мгновенно стала популярной. Он ввел неологизм «фрактал», чтобы объединить все эти странные объекты под одним термином.

«Я придумал фрактал от латинского прилагательного «fractus». Соответствующий латинский глагол «frangere» означает «ломать», «создавать нерегулярные фрагменты». Поэтому в дополнение к значению «фрагментированный» (как в словах «дробь» [fraction] и «преломление» [refraction]), «fractus» также означает «нерегулярный», причем оба значения сохраняются во фрагменте» [2].

Фракталы мгновенно привлекли внимание художников, что привело к появлению новой формы цифрового искусства, которая быстро стала популярной как внутри, так и за пределами художественных и научных сообществ. Музыкальный интерес последовал почти одновременно, сосредоточившись в основном на области алгоритмической композиции. Вследствие этого возникли сложные вопросы: Фрактальное искусство – новый прорыв? Станет ли фрактальное искусство осуществлением миссии искусства? И даже: приближаемся ли мы к раю?

Что такое фрактал? Фрактальная геометрия (и немного топологии)

Топологическая размерность множества определяется как количество независимых параметров, необходимых для описания точки в этом множестве. Например, точка на плоскости описывается двумя независимыми параметрами (также известными как декартовы координаты точки), в этом смысле плоскость двумерна. По определению, топологическая размерность всегда является натуральным числом. Однако топологическая размерность ведет себя совершенно неожиданным образом на некоторых сильно нерегулярных множествах, таких как фракталы. Размерность Хаусдорфа предлагает другой способ определения размерности для таких множеств.

Пусть F – фрактал в трехмерном пространстве, а N(r) – минимальное число шаров радиуса меньше или равного r, необходимое для полного покрытия F по объему. Очевидно, что с уменьшением r N(r) становится больше. Грубо говоря, когда r стремится к 0, N(r) становится пропорциональным 1/r^d, где d – действительное число. Число d называется размерностью Хаусдорфа для F. Размерность Хаусдорфа по сути определяет способность покрытой поверхности (в нашем случае фрактала) заполнять пространство; кроме того, она уточняет понятие топологической размерности, связывая её с другими свойствами пространства, например, такими как объём.

Интересно, что размерность Хаусдорфа чаще всего является дробной, а не целой. Например, если мы рассматриваем твёрдую сферу, то её размерность Хаусдорфа равна её топологической размерности. Однако если вместо этого мы рассмотрим полую сферу, то полученная размерность Хаусдорфа в конечном итоге будет числом между 2 и 3. Хотя это несколько необычно, но хаусдорфова размерность чаще всего является дробью, а не целым числом. Поэтому фракталы и другие сильно нерегулярные множества также имеют дробную размерность, которая обычно больше, чем их топологическая размерность.

Существует несколько тесно связанных между собой понятий возможных дробных размерностей. Обычно их называют фрактальными размерностями. Обратите внимание, что слово «фрактал» является неологизмом и как таковое семантически не связано со словом «дробный». Мандельброт формально определил фрактал как множество с размерностью Хаусдорфа, строго превышающей его топологическую размерность. Однако такое определение оказалось неудовлетворительным, поскольку оно исключало ряд множеств, которые явно должны рассматриваться как фракталы.

Как отмечает Кеннет Фальконер, «определение «фрактала» следует рассматривать так же, как биолог рассматривает определение «жизни» [—] просто как список свойств, характерных для живого существа [—] большая часть живых существ обладает большинством характеристик из этого списка, хотя есть живые объекты, которые являются исключением для каждой характеристики». Аналогично кажется лучшим рассматривать фрактал как множество, обладающее списком свойств, а не искать точное определение, которое почти наверняка исключит некоторые интересные случаи» [3].

Таким образом, фрактал F определяется как геометрический объект, в общем случае обладающий следующими свойствами:

1. F имеет тонкую структуру, т.е. детализацию на произвольно малых масштабах.
2. F слишком нерегулярен, чтобы его можно было описать традиционным геометрическим языком, как локально, так и глобально.
3. F имеет некоторую форму самоподобия, по крайней мере приблизительно или стохастически.
4. F имеет «фрактальную размерность» (определенную каким-либо образом), которая больше, чем его топологическая размерность.
5. F имеет простое и рекурсивное определение в большинстве представляющих интерес случаев.

Фракталы обычно генерируются при помощи трех методов:

1. Фракталы времени побега [escape-time fractals]: определяются рекуррентным соотношением в каждой точке пространства.
2. Системы итерированных функций (IFS): существует фиксированное правило геометрической замены.
3. Случайные фракталы: они генерируются стохастическими, а не детерминированными процессами.

Фракталы также можно классифицировать по их самоподобию. Во фракталах выделяют три типа самоподобия, которые перечислены ниже в прямом соответствии с представленными выше методами генерации:

1. Квазисамоподобие: фрактал выглядит приблизительно (но не точно) идентичным в разных масштабах. Квазисамоподобные фракталы содержат маленькие копии всего фрактала в искаженной и вырожденной форме. Это свободная форма самоподобия.

2. Точное самоподобие: фрактал выглядит идентичным в разных масштабах. Это самый сильный тип самоподобия.

3. Статистическое самоподобие: фрактал имеет числовые или статистические показатели, которые сохраняются в разных масштабах. Это самый слабый тип самоподобия.

Теория хаоса

Теория хаоса описывает поведение системы нелинейных динамических уравнений при итерациях. Итерация – это процесс, при котором выходное значение возвращается в систему в качестве нового входного значения. Этот процесс повторяется бесконечно много раз. Каждый шаг даёт значение, которое представляет собой точку в n-мерном пространстве (n определяется количеством переменных в уравнениях). Орбита системы определяется как совокупность этих точек во времени. Аттрактор системы – это множество, к которому сходится орбита системы.

Существует три категории поведения, в которые может попасть система после итерации: постоянное, когда все точки на орбите стремятся к стабильному значению; колебательное, когда все точки на орбите принадлежат повторяющемуся множеству; и хаотическое, когда ни одна точка на орбите не посещается дважды за конечный промежуток времени. Последняя категория поведения является наиболее интересной.

Система блуждает по ряду точек, часто возвращаясь в близкие, но никогда не совпадающие точки, и её аттрактор, с геометрической точки зрения представляющий собой сложный набор с фрактальными характеристиками, называется странным аттрактором или фрактальным аттрактором. Странные аттракторы на самом деле являются фракталами, принадлежащими к числу наиболее интересных и красивых. Существенной особенностью странного аттрактора является его чувствительность к начальным условиям, т.е. незначительные различия в начальных значениям системы могут привести к резким, неожиданным результатам после определенного числа итераций [4].

Другими словами, возникает хаос! Исторически «странные» структуры существовали в математике и до фракталов. Их характеризовали как «патологические», поскольку они не соответствовали шаблонам Евклида. Однако:
«создавшие (их) математики считали их важными для того, чтобы показать, что мир чистой математики содержит богатство возможностей, выходящих далеко за пределы простых структур, которые они видели в Природе. [—] Теперь, как отмечает Мандельброт, […] природа сыграла с математиками шутку. Математикам XIX века, возможно, не хватало воображения, но природе – нет. Те же патологические структуры, которые математики изобрели, чтобы освободиться от натурализма XIX века, оказываются присущими знакомым объектам вокруг нас» [5]. Масштабное самоподобие – самое важное свойство фрактала; это «странный аттрактор» динамической системы, определяемой математикой, искусством и природой.

Добро пожаловать во Фракталандию!

Фрактальное искусство создается путем вычисления фрактальных математических функций (алгоритмов) и преобразования результатов в цифровые неподвижные или анимированные изображения и музыку. Фрактальные изображения представляют собой визуальное представление алгоритмических данных, а фрактальная музыка отображает результаты вычислений в музыкальных тонах или других звуках. Хотя определяющим результат работы фактором является инициатива художника/программиста, фрактальное искусство подверглось резкой критике касательно того, следует ли его считать формой искусства из-за его вычислительного происхождения.

Фрактальные изображения – это цифровые изображения, которые состоят либо из одного фрактала, либо из нескольких полуфрактальных и нефрактальных объектов. Стали широко доступны программные инструменты, с помощью которых художник может алгоритмически генерировать фрактал, применять цветовые узоры и составлять цифровые изображения. Используемые алгоритмы относятся к трем методам генерации, представленным в предыдущем разделе, что позволяет художнику выбирать тип самоподобия и уровень сложности. Одной из самых популярных программ для генерации фракталов является программа «Ultra Fractal».

Ее инновационной особенностью является встроенная возможность наложения слоев; кроме того, она стала первой программой, которая полностью передала контроль над изображением в руки пользователя. Следует отметить, что раскрашивание фрактального изображения является важной частью процесса. С геометрической точки зрения фрактальный объект состоит из «окрестностей» различной значимости. Компьютеры генерируют фрактал путем применения различных цветов к различным уровням важности, в результате чего получаются выдающиеся красочные изображения, которые поражают воображение.

Две подобласти фрактальных изображений – фрактальное пламя и фрактальные пейзажи. Фрактальное пламя в основном создается с помощью IFS (Iterated Functions System) – метода «Системы Итерируемых Функций» который появился в середине 80-х годов как простое средство получения фрактальных структур. Фрактальные ландшафты создаются с помощью стохастических алгоритмов. […] Наконец, последовательность фрактальных изображений создаёт так называемую фрактальную анимацию.

Математикам XIX века, возможно, не хватало воображения, но природе – нет. Те же патологические структуры, которые математики изобрели, чтобы освободиться от натурализма XIX века, оказываются присущими знакомым объектам вокруг нас.

Фрактальная музыка – это преимущественно область алгоритмической композиции. Для задания композиционного процесса алгоритмы генерации фракталов применяются к высоте тона, динамике, длительности, времени и другим параметрам звука. Существует несколько типов фрактальной музыки в зависимости от используемых методов и программного обеспечения. Такие программы как MusiNum и Gingerbread генерируют музыку, используя исключительно фрактальную математику, преобразования осуществляются в соответствии с выбираемым музыкальным строем.

Однако большинство программ используют фракталы в совокупности с множеством других алгоритмических методов. В других случаях композиторы используют фрактальную музыку в качестве отправной точки, чтобы затем развить композиционную тему при помощи обычных инструментов, сэмплов и других звуков.

Еще один способ создания фрактальной музыки – использование итерированных систем нелинейных динамических уравнений в качестве алгоритмов генерации нот. Результат напрямую зависит от поведения системы. Очевидно, что неизменное поведение [constant behavior] не даст интересных музыкальных результатов. Колебательное поведение может создавать интересные повторения, если период (количество отдельных точек в повторяющемся наборе) достаточно велик, но на практике такой набор обычно довольно мал, что приводит к тому, что мелодии лишь кружатся между несколькими тонами. Именно хаотическое поведение представляет наибольший музыкальный интерес. Музыкальная интерпретация странного аттрактора в результате чем-то напоминает «вариации на тему». Создаваемый материал имеет высокую степень корреляции с прошлым, но в то же время всегда порождает что-то новое.

Фракталы существовали всегда!

Задолго до математического обоснования фракталов и хаоса фрактальные узоры, самоподобие, хаотические структуры и бесконечность использовались художниками, скульпторами и композиторами как для мотивации, так и в качестве инструмента количественной оценки.

В конце 1940-х годов Джексон Поллок при создании нескольких абстрактных полотен использовал два революционных метода, связанных с хаотическими структурами. В первом случае он задействовал всё своё тело, чтобы привнести в свои мастерские движения широкий диапазон размаха. Во втором случае он наносил краску, позволяя ей свободно капать на холст.

Более того, электронная деконструкция картин Поллока на составляющие их цветные слои показала, что каждый из отдельных слоев состоит из однородного фрактального узора [8]. Нидерландский художник Мауриц Корнелис Эшер (1898-1972) создал свои знаменитые мозаичные рисунки, вдохновленный идеями бесконечного повторения и масштабируемого самоподобия, часто создавая оптические иллюзии. На картине Сальвадора Дали «Видение войны» изображена фрактальная прогрессия все более и более мелких масок смерти.

Самоподобие изобилует в канонических произведениях западной музыки. Основные примеры – каноны и фуги. Канон – это контрапунктическая композиция, в которой используется мелодия с одной или несколькими имитациями, исполняемыми через определенную длительность (обычно один такт). Начальная мелодия называется лидирующей, а имитация – ведомой. Ведомая мелодия является либо точной копией лидера, либо его трансформацией, поэтому существует несколько различных типов канонов. Фуга – это более сложная форма контрапунктической композиции, где одна главная тема, субъект, звучит в последовательном подражании в каждом голосе.

Изучение знаменитых канонов и фуг И. С. Баха подтверждает мастерское использование самоподобия и масштабирования. Музыка Бетховена и Моцарта также состоит из подобных элементов. Как отметил Мандельброт, «музыка проявляет фрактальные характеристики из-за своей иерархической природы». [9]. Требуется ли продолжительная зависимость и самоподобие для того, чтобы музыка стала «приятной» и «гармоничной»?

В конце концов, это фрактальный мир, не так ли?

С созданием фрактальной геометрии и теории хаоса вскоре стало ясно, что это полезные математические инструменты для описания природы. Ученые продолжили изучать природные узоры в объектах под совершенно новым углом зрения, и результаты оказались более чем просто интересными. Нерегулярность, хаос, резкие изменения, прерывистость, самоподобие, масштабирование: все это определяет внутреннюю и внешнюю красоту, а также гармонию природы и жизни.

Деревья, ветви, листья, корни растений, цветная капуста, снежинки, алмазы, береговые линии, горы, облака, звезды, небо, скопления галактик – фрактальные аттракторы описывают видимые природные формы. Погода, Солнечная система, тектоника плит, турбулентные жидкости, рост населения, экономика – всё это примеры хаотических динамических систем. Мозг и бронхиальные доли также являются примерами телесных структур с элементами самоподобия и масштабирования.

В 1982 году Бенуа Мандельброт написал свое фундаментальное сочинение «Фрактальная геометрия природы», в котором представил революционные идеи в математической, философской и художественной форме. Сочинение оказало сильнейшее влияние на многих учёных и художников. Новаторская концепция Мандельброта заключалась в успешном изображении природного узора фрактальным множеством. По словам Мандельброта, «многие грани природы могут быть описаны только с помощью фракталов […] Узоры природы нерегулярны и фрагментарны […] самоподобие – это […] ткань Природы» [11].

Новая научная эстетика

Теория хаоса открыла совершенно новую эстетику в науке. Традиционно наука рассматривала отношения между наблюдателем и наблюдаемым как чисто «объективные». Однако теория хаоса резко опровергла это предположение, показав, что такие отношения обладают хаотической динамикой и, следовательно, являются «субъективными». С другой стороны, художники всегда понимали, что изменение одной небольшой части картины или музыкальной композиции может разрушить, либо преобразить произведение. Хаос объединил два мира – искусство и науку – и приблизил нас к более глубокому пониманию природы [12].

Справочник «American Heritage Dictionary» даёт следующее определение искусства: 1. это человеческая попытка имитировать, дополнить, изменить или противодействовать плодам природы; и 2. это сознательное производство или расположение звуков, цветов, форм, движений или других элементов, чтобы воздействовать на чувство прекрасного, в частности, создать прекрасное при помощи графических или пластичных средств [13].

Фрактальное искусство, очевидно, ближе других видов искусства соответствует этому определению по причине своей релевантности естественным процессам. Природа формирует узоры, находящиеся где-то между порядком и хаосом; некоторые из них упорядочены во времени, но беспорядочны в пространстве, другие упорядочены в пространстве, но беспорядочны во времени; это фрактальные узоры [14]. Мы встречаем эти паттерны повсюду в реальном мире. Даже реакция человека на природные явления в большинстве случаев непредсказуема.

Традиционно наука рассматривала отношения между наблюдателем и наблюдаемым как чисто «объективные». Однако теория хаоса резко опровергла это предположение, показав, что такие отношения обладают хаотической динамикой и, следовательно, являются «субъективными».

В истории культуры искусство было либо полностью упорядоченным (классицизм, кубизм), либо полностью беспорядочным (дада, сюрреализм); кажется, фрактальное искусство заполняет промежуток между ними. Ожидается, что в области музыки фрактальные алгоритмы создадут более реалистичные естественные звуки и более утончённые мелодии, чем обычные алгоритмические подходы. Музыка, создаваемая хаотическими нелинейными динамическими системами, оценивается как более интересная с эстетической точки зрения, чем музыка, полученная с помощью других стохастических алгоритмов, например, таких как цепи Маркова [15].

Фрактальная музыка производит паттерны, которые рождаются в результате естественных процедур, поэтому она гармонична и прекрасна в своей сложности. Последующая обработка таких паттернов – либо как последовательностей музыкальных событий, либо как сложных частотных спектров – сулит создание музыкальных произведений, которые откроют новые горизонты в музыкальной композиции. Поскольку фрактальные структуры обнаруживаются в природе – в природе самого звука – и в нашем восприятии музыкальной красоты, фрактальная музыка станет следующей музыкальной революцией [16].

Заключение

Непрерывность и бесконечность характеризуют саму природу. Поэтому изображение и звук, как неотъемлемые части природы, и, следовательно, искусство и музыка, могут быть переосмыслены через них, обретая совершенно новое видение и миссию.

Современная математика предоставляет для этого необходимые инструменты, как научные, так и художественные, через фрактальную геометрию и теорию хаоса. Фрактальное искусство находится в той самой точке, где природа Искусства встречается с искусством Природы. Его бесконечные (но не самоподобные!) возможности еще предстоит исследовать.

Адаптированный перевод с английского А.Н. Липова. Перевод выполнен по изданию: Charalampos Saitis Fractal Art: Closer to Heaven? Modern Mathematics, the art of Nature, and the nature of Art. In: The Aesthetics of Interdisciplinarity: Art and Mathematics (pp. 153-163).

Приложение

Возможности фракталов широко используются не только в художественной графике. При помощи фрактальных функций часто описывают свойства сложных природных объектов: турбулентных потоков, географических ландшафтов и т.п.

Примеры итерации природных фракталов:

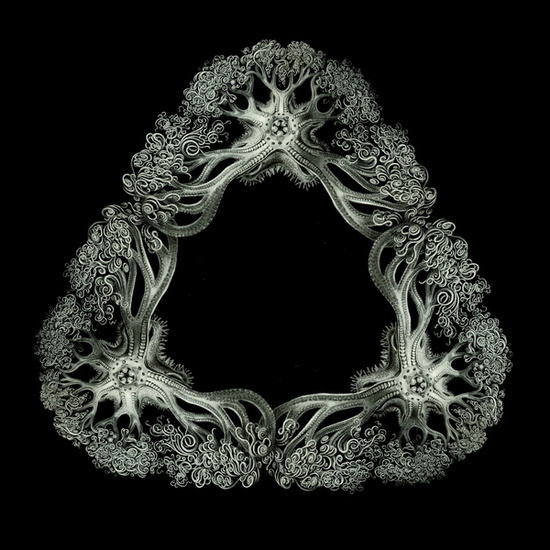
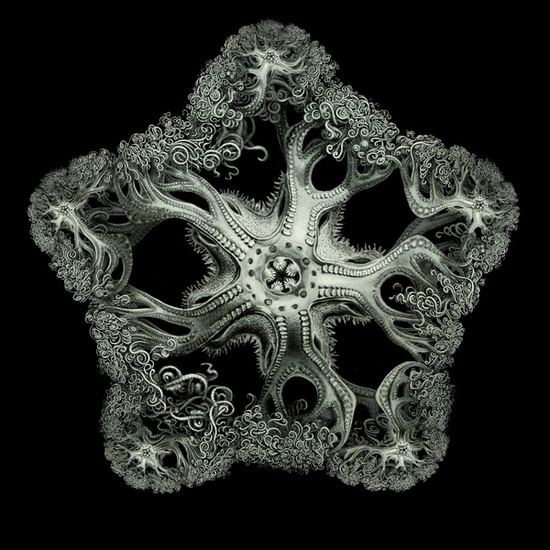
Фрактальные композиции, полученные на основе компьютерного рендеринга:

Мандельбульб

Мандельбульб – трехмерный фрактал, сконструированный в 2009 году Полом Нюландером и Дэниелом Уайтом,  трехмерное воплощение множества Мандельброта.

Фракталы и космос

Более того, современные научные данные свидетельствуют о том, что и Вселенная, возможно, является фракталом. Так, группа итальянских и российских астрономов, проанализировав данные, полученные в рамках Слоановской программы цифрового обзора неба (Sloan Digital Sky Survey), пришла к выводу, что материя во Вселенной распределена в виде фрактала.

Звездная материя туманностей и скоплений галактик удивительнейшим образом напоминает некоторые из искусственно созданных красочных фракталов на экране компьютера. При фотографировании с использованием телескопов большого разрешения на снимках появляются красочные картины далекого Космоса со сложной топологией и цветовыми соотношениями, искусству сотворения которых позавидовал бы любой художник:

Фракталы и музыка

Хотя существовали музыкальные теории, определявшие, как бы мы сейчас сказали, фрактальность музыкальных форм и до открытия Мандельброта (так, например, Дебюсси открыл неизведанное звуковое поле и способ соединения звуков, будь то последовательным, то есть мелодичным или одновременным, то есть гармоническим) фрактальная музыкальная форма возникла в середине ХХ века. Фрактальная музыка существует между математическими уравнениями и теорией хаоса.

К числу наиболее известных сегодня композиторов, использовавших алгоритмические процедуры и элементы фрактальной музыки  можно отнести Джона Кейджа, Чарльза Доджа, Брайана Ино, Шона Бута и Роба Браунов, Карлхайнца Эссла, Лежарена Хиллера, Готфрида Майкл Кенига, Пола Лански, Эдуардо Миранда Рек, Яниса Ксенакиса, Лори Шпигель и мн. др. Музыканты начали исследовать возможности звуковых фракталов, пытаясь уйти от традиционных областей музыки, чтобы выразить волновые формы фракталов, используя целый ряд необычных с художественной точки зрения инструментариев, как, например, изменения плотности воздуха с течением времени.

При этом фрактальный и генеративный подход к синтезу звука и построению музыкальных произведений открывает совершенно новые горизонты для композиторов. Появилась возможность создавать музыкальные и акустические произведения, которые при каждом проигрывании изменялись и трансформировались. Звук стал пластичной структурой. Композиторы и художники получили дополнительные технологические возможность резать, обрабатывать, видоизменять звук в студии. Примеры включают как гармонические мелодии, так и психоделические и совершенно необычные, не имеющие аналогов в природе звучания, которые могут быть выражены и сгенерированы с помощью манипуляций и быть следствием неясных даже для пользователя фрактальных вибраций и превращений.

По мере развития акустических и музыкальных технологий возникают и новые, неизвестные ранее звуковые возможности фракталов. Так, например, визуализация фрактальной музыки на основе таких визуализаторов музыки как: VSDC, MusicVid, Vizzy, Headliner, WoFox, Renderforest, Videobolt, Songrender, Specterr, производит вот такие необычные красочные изображения:

Фрактальная эстетика природы и искусства

Как можно было увидеть, фрактальная сложность Мандельброта определяет красоту природы, обуславливая не только ее морфологическую, но и «визуальную» сложность. Многие природные, в том числе биологические, структуры являются фрактальными (или фракталоподобными). Фракталы сложны, потому что обладают структурным сходством в разных масштабах. Фрактальные узоры, кажется, существуют повсюду.

Фрактальные структуры, которые повторяются в различных масштабах, не только составляют естественную среду, но и присутствуют также в художественных произведениях, которые могут считаться считаются высокоэстетичными, и, видимо, уже правомерно говорить не только об изобразительности, красоте, но и художественности фрактальных структур.

Фракталы преобладают в природных ландшафтах (например, в деревьях, горах, облаках, реках) и в то же время, например, картины Джексона Поллока отражают морфологию фрактальности в том смысле, что техника неоднократных наслоений краски художником создает фрактальную структуру.

Художники и композиторы уже обсуждают возможности генерации, создания цветной фрактальной музыки и даже включения в музыкальное произведение цветных (белого, розового, коричневого) шумов, когда каждое акустическое значение не зависит от предыдущего, как в коричневом шуме (также называемом случайным блужданием или «блужданием пьяницы»), а акустические события генерируется случайным образом вокруг предыдущего значения и, в то же время не зависят от него.

При этом сложность, структурная насыщенность, многообразие и яркость, например, визуальных фрактальных изображений поразительна и не может быть объяснена только лишь сложностью генерации, применяемой на основе современных компьютерных технологий. На фото ниже представлены необыкновенно яркие фрактальные изображения, также полученные на основе компьютерного рендеринга:

Поэтому без сомнений можно утверждать, что с проникновением в искусство фрактального принципа и созданием на его основе высокотехнологичной художественной среды, приоткрывается дверь в область, обладающую неизведанными и не освоенными ранее художественной культурой принципами и инструментарием. Пожалуй, не будет преувеличением сказать, что мы стоим сегодня на пороге создания новых, неизведанных ранее художественных систем, технологические и изобразительные возможности которых еще только предстоит открыть в искусстве.